问题
计算题
在平直公路上，甲车在前以υ1=12m/s的速度匀速行驶，乙车在后以υ2=8m/s的速度匀速行驶。当两车相距L=24m时，甲车以大小为2m/s2的加速度开始刹车，则
（1）相遇前，甲车刹车后经时间t1为多长时两车距离最大？并求最大距离sm；
（2）甲车刹车后经时间t为多长时乙车追上甲车？
答案
解：（1）两车距离最大时乙车的速度与甲车的速度相等，即
υ1′=υ2，υ1′=υ1+at1
得t1=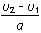
=2s，s2=υ2t1，s1=
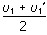t1
sm=L+s1-s2
得sm=28m
（2）0=υ1+at2，得甲车刹车的时间t2=6s
-υ12=2as1′，甲车刹车位移大小s1′=36m
甲车停下时乙车的位移大小s2′=υ2t2，s2′=48m
由于s2′<L+s1′
所以甲车停止后乙车再去追甲车
追上时乙车的总时间大小t=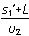
=7.5 s