问题
选择题
AE、CF是锐角三角形ABC的两条高，如果AE：CF=3：2，则sinA：sinC等于（ ）
A．3：2
B．2：3
C．9：4
D．4：9
答案
如图．
sinA=
，sinC=CF AC
，AE AC
则sinA：sinC=
=CF AC AE AC
，CF AE
又∵AE：CF=3：2，
∴sinA：sinC=2：3．
故选B．
搜题请搜索小程序“爱下问搜题”
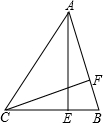
AE、CF是锐角三角形ABC的两条高，如果AE：CF=3：2，则sinA：sinC等于（ ）
A．3：2
B．2：3
C．9：4
D．4：9
如图．
sinA=
，sinC=CF AC
，AE AC
则sinA：sinC=
=CF AC AE AC
，CF AE
又∵AE：CF=3：2，
∴sinA：sinC=2：3．
故选B．