参考答案：

将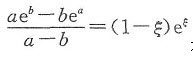左边的分子、分母同除ab，归结证明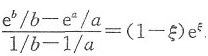

可用柯西中值定理证之．

证 设f(x)=e^x/x，g(x)=1/x显然f(x)，g(x)在[a，b]上满足柯西中值定理的条件，故存在ξ∈(a，b)，使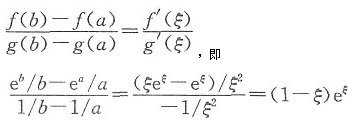

即

ae^b-be^a=(1-ξ)e^ξ(a-b)．

注意 为找到使用柯西中值定理的两函数，有时需用两端点坐标的乘积(或其函数乘积)同除分子、分母，使之能化成两函数在端点处的差值比．