问题
填空题
在△ABC中,AB=5cm,AC=4cm,tan∠ABC=
|
答案
分为两种情况:①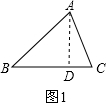
如图1,过A作AD⊥BC于D,
∵tan∠ABC=
=3 4
,AD BD
设AD=3xcm,BD=4xcm,
在Rt△ADB中,由勾股定理得:(3x)2+(4x)2=52,
解得:x=1,
即BD=4x=4(cm),AD=3x=3(cm),
在Rt△ADC中,由勾股定理得:DC=
=AC2-AD2
=42-32
(cm),7
∴BC=BD+DC=(4+
)cm;7
②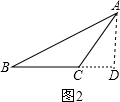
如图2,过A作AD⊥BC交BC延长线于D,
∵tan∠ABC=
=3 4
,AD BD
设AD=3xcm,BD=4xcm,
在Rt△ADB中,由勾股定理得:(3x)2+(4x)2=52,
解得:x=1,
即BD=4x=4(cm),AD=3x=3(cm),
在Rt△ADC中,由勾股定理得:DC=
=AC2-AD2
=42-32
(cm),7
∴BC=BD-DC=(4-
)cm;7
故答案为:4+
或4-7
.7
