问题
填空题
设c为任意常数，以y=ex2+cx为通解的微分方程为（）。
答案
参考答案：xy’-ylny=x2y
解析：
直接对通解求导数，得到y的一阶导数所满足的方程，即为所求的方程．
由y=ex2+cx有
lny=x2+cx．
为消掉常数c，将上式化为
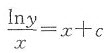
两边对x求导得到
化简得到xy’-ylny=x2y．
搜题请搜索小程序“爱下问搜题”
设c为任意常数，以y=ex2+cx为通解的微分方程为（）。
参考答案：xy’-ylny=x2y
解析：
直接对通解求导数，得到y的一阶导数所满足的方程，即为所求的方程．
由y=ex2+cx有
lny=x2+cx．
为消掉常数c，将上式化为
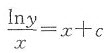
两边对x求导得到
化简得到xy’-ylny=x2y．