问题
计算题
物体A做匀速直线运动，速度为vA=4 m/s，2 s后物体B从同一位置与A同方向做匀加速直线运动，v0=0，a=2 m/s2，求：
(1)B出发后，经过多少时间追上A？
(2)B追上A时，离出发点多远？
(3)B追上A前，最远距离是多少？
答案
解：(1)设B出发后经时间t追上A，依据题意，B追上A时满足条件：vA(t+2s)=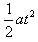
代入数据，得4(t+2 s)=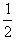
×2t2
解得t=(2+
) s≈5.46 s
(2)B 上A时离出发点的距离是x=vA(t+2s)=[4×(2+5.46)] m=29.84 m
(3)A、B距离最远时，应有vA=vB，即4 m/s=2 m/s2·t'，t'=2 s
此时△x=xA-xB=vA(t'+2s)-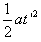
=12 m