问题
解答题
在一次购物抽奖活动中，假设某10张奖券中有一等奖卷1张，可获价值50元的奖品；有二等奖卷3张，每张可获价值10元的奖品；其余6张没有奖。某顾客从这10张中任抽2张，求：（1）该顾客中奖的概率；（2）该顾客获得的奖品总价值X（元）的分布列和数学期望。
答案
(1) 
(2)
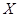 | 0 | 10 | 20 | 50 | 60 |
 |  |  |  |  | |
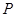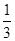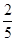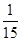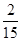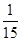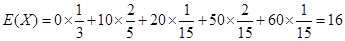。该顾客获得的奖品总价值X（元）的数学期望为16。
题目分析：解：（1）记顾客中奖为事件A.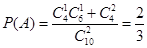
,即该顾客中奖的概率为。
（2）X所有可能的取值为（单位：元）：0,10,20,50,60.且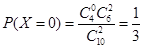
,
,
,
,
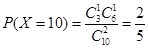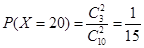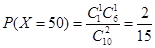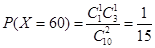.故X的分布列为
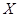| 0 | 10 | 20 | 50 | 60 |
| | | | | |
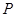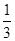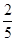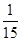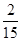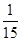。该顾客获得的奖品总价值X（元）的数学期望为16。
点评：主要是考查了古典概型的概率公式的运用，以及离散型随机变量的分布列的求解，属于中档题。