问题
解答题
（本题满分14分）
已知箱中装有4个白球和5个黑球，且规定：取出一个白球的2分，取出一个黑球的1分．
现从该箱中任取 ( 无放回 ) 3个球，记随机变量X为取出3球所得分数之和．
(Ⅰ) 求X的分布列；
(Ⅱ) 求X的数学期望E(X)．
答案
(Ⅰ)所求X的分布列为
| X | 3 | 4 | 5 | 6 |
| P |  |  |  |  |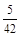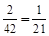
(Ⅱ) 所求X的数学期望E(X)为：
E(X)＝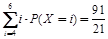
．
本题主要考查随机事件的概率和随机变量的分布列、数学期望等概念，同时考查抽象概括、运算能力，属于中档题．
（1）X的可能取值有：3，4，5，6，求出相应的概率可得所求X的分布列；
（2）利用X的数学期望公式，即可得到结论．
解：(Ⅰ) X的可能取值有：3，4，5，6．
； 
；
； 
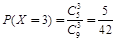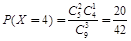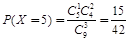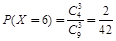． ………………8分
故所求X的分布列为
| X | 3 | 4 | 5 | 6 |
| P | | | | |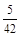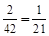
(Ⅱ) 所求X的数学期望E(X)为：
E(X)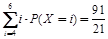＝． ………………14分