问题
计算题
有一质量为M、长度为l的矩形绝缘板放在光滑的水平面上，另一质量为m、带电量的绝对值为q的物块（视为质点），以初速度v0从绝缘板的上表面的左端沿水平方向滑入，绝缘板周围空间是范围足够大的匀强电场区域，其场强大小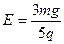
，方向竖直向下，如图所示。已知物块与绝缘板间的动摩擦因数恒定，物块运动到绝缘板的右端时恰好相对于绝缘板静止；若将匀强电场的方向改变为竖直向上，场强大小不变，且物块仍以原初速度从绝缘板左端的上表面滑入，结果两者相对静止时，物块未到达绝缘板的右端。求：
(1)场强方向竖直向下时，物块在绝缘板上滑动的过程中，系统损失的动能；
(2)场强方向竖直向下与竖直向上时，物块受到的支持力之比；
(3)场强方向竖直向上时，物块相对于绝缘板滑行的距离。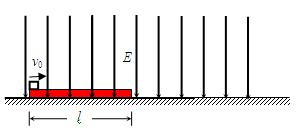
答案
(1)场强方向竖直向下时，由系统动量守恒，有：
①
由能量守恒，有（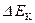
：产生热量；Ｆf ：m与M间的摩擦力；s：m与M相对位移；
v：A、B共同速度）：
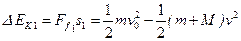②
由①②式得: 
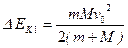③
同理，场强方向竖直向上时，动量仍守恒，可推出：
④
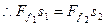5
依题意：s1 > s2，故Ff 2 > Ff 1
而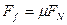
6
∴FN2 > FN1
说明第一次电场力方向竖直向上，第二次电场力方向竖直向下(可判断物块带负电)
（2）s2=