问题
填空题
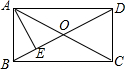
在矩形ABCD中,O是两条对角线的交点,AE⊥BD于点E,若0E:OD=1:2,AE=
|
答案
∵四边形ABCD是矩形,
∴AC=BD,OA=CO,BO=OD,
∴AO=OD=OC=OB,
∵0E:OD=1:2,
∴OD=2OE=OB,
∴OE=BE,
∵AE⊥BD,
∴AO=AB=OB,
∴△AOB是等边三角形,
∴∠AOB=60°,
在Rt△AOE中,sin60°=
,AE OA
∴OA=
=2(cm),3 sin60°
∴OD=OA=OB=2cm,OE=BE=1cm,
∴DE=2cm+1cm=3cm,
故答案为:3.