问题
解答题
在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标。
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率。
答案
解:(1)∵列表如下:

∴点M坐标的所有可能的结果有九个:
(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3); (2)点M在直线y=x上的有3个:
(1,1),(2,2),(3,3),
点M在直线y=x上的概率P=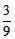 =
=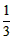 ;
;
(3)∵画树状图如下:
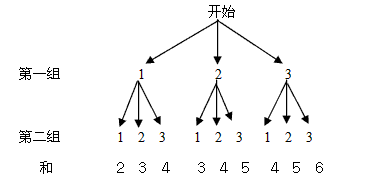
偶数有5个,
∴点M的横坐标与纵坐标之和是偶数的概率P=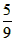 。
。
