问题
问答题
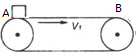
如图所示,水平传送带AB长L(足够长),以v0的速度向右匀速运动(传送带的传送速度恒定),质量为m的小木块无初速度放在传送带的最左端A点,小木块经过t1后与传送带速度大小相等.求:
(1)小木块与传送带间的动摩擦因数μ是多大?
(2)小木块在传送带上从A点运动到B点的时间T是多少?
答案
(1)小木块刚放上皮带时,速度小于皮带的传送速度,即相对皮带向后运动,受到向前的摩擦力,重力与支持力平衡,故合力等于摩擦力;
f=μFN,FN=mg=μmg
根据牛顿第二定律得,a=
| f |
| m |
又因为a=
| vt |
| t1 |
| v0 |
| t1 |
所以μ=
| v0 |
| t1g |
故小木块与传送带间的动摩擦因数为
| v0 |
| t1g |
(2)小木块在传送带上先作匀加速直线运动,后作匀速直线运动;
匀加速位移,x1=
| . |
| v |
| v0 |
| 2 |
匀速位移,x2=L-x1;
匀速时间,t2=
| x2 |
| v0 |
| 2L-v0t1 |
| 2v0 |
总时间,T=t1+t2=
| 2L+v0t1 |
| 2v0 |
故小木块在传送带上从A点运动到B点的时间T是
| 2L+v0t1 |
| 2v0 |
