在水平光滑的绝缘桌面内建立如图所示的直角坐标系,第Ⅰ、Ⅱ象限有方向垂直桌面的匀强磁场.第Ⅲ、Ⅳ象限有大小为E的匀强电场,方向与x轴成45°。现把一个质量为m,电量为q的正电荷从坐标为(0,-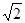 b)的M点处由静止释放,电荷以一定的速度第一次经x轴进入磁场区域。经过一段时间,从坐标原点O再次回到电场区域。求:(不计电荷的重力)
b)的M点处由静止释放,电荷以一定的速度第一次经x轴进入磁场区域。经过一段时间,从坐标原点O再次回到电场区域。求:(不计电荷的重力)

(1)电荷第一次经x轴进入磁场时的速度;
(2)磁感应强度的大小;
(3)粒子从M到O运动时间。
(1)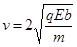 与x轴成45°(2)
与x轴成45°(2)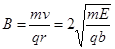 (3)
(3)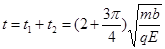
(1)粒子从静止沿电场方向进入磁场,到达x轴上的N点,N点的
坐标是(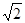 b,0)
b,0)
由几何知识可知粒子从M到N的位移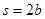 ……….. ….. ….. …..……..(1分)
……….. ….. ….. …..……..(1分)
根据动能定理有: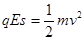 ………….. ………….. ….. ….. ….. ….. …(2分)
………….. ………….. ….. ….. ….. ….. …(2分)
解得进入磁场时的速度 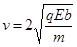 ……….. ….. ….. …..….. ….. …..…(1分)
……….. ….. ….. …..….. ….. …..…(1分)
速度方向与电场方向一致,即与x轴成45°.. ….. ………..….. ….. …..…(1分)
(2)粒子进入磁场做匀速圆周运动,轨迹如图所示。
由几何关系可得圆周运动的半径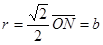 ………………………..(2分)
………………………..(2分)
由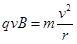 ……………………………….. ……………………………(2分)
……………………………….. ……………………………(2分)

解得 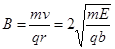 …………….. ………………………………………(1分)
…………….. ………………………………………(1分)
(3)电荷在电场中的加速度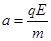 …………………
…………………
电荷在电场中的运动时间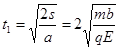 ………(2分)
………(2分)
电荷在磁场中的运动周期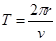 ………………
………………
它在磁场中运动的时间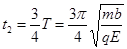 …(2分)
…(2分)
所以,电荷运动的总时间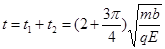 …………(1分)
…………(1分)
