问题
选择题
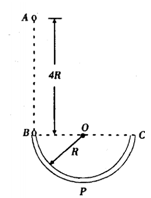
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形，固定在竖直面内，管口B,C的连线水平。质量为m的带正电小球从B点正上方的A点自由下落A,B两点间距离为4R。从小球（小球直径小于细圆管直径)进人管口开始,整个空间中突然加上一个斜向左上方的匀强电场,小球所受电场力在竖直方向上的分力方向向上,大小与重力相等，结果小球从管口 C处离开圆管后，又能经过A点。设小球运动过程中电荷量没有改变，重力加速度为g,求：
（1）小球到达B点时的速度大小；
（2）小球受到的电场力大小；
(3) 小球经过管口C处时对圆管壁的压力。
答案
（1）
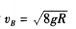
(2) 
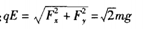
(3) 
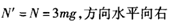
（1）小球下落过程只有重力做功，根据机械能守恒定律列式求解；
（2）小球从B到C过程，只有电场力做功，根据动能定理列式；小球离开C点后，竖直方向做匀速运动，水平方向做加速运动，根据平抛运动的知识列式求解；
（3）小球经过C点时，电场力和支持力的合力提供向心力，根据牛顿第二定律列式即可．
解：（1）小球从开始下落到管口B，机械能守恒：mg?4R=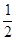
m
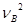解得vB=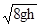
（2）设电场力的竖直向上分力为Fy，水平分力为Fx，则Fy=mg
从B到C，由动能定理：-Fx?2R=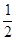m(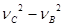
---------------①
小球从管口C到A，做类平抛，竖直方向匀速运动 y=4R=VC?t----------②
水平方向做匀加速运动x=2R=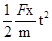
-----③
由①②③得Fx=mg 故电场力大小F=
mg 方向与水平向左成450斜向上．
（3）球在管口C处由牛顿定律：Fx+N=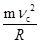
得N=3mg
点评：本题关键运用正交分解法，将小球的运动沿水平方向和竖直方向正交分解，然后运用牛顿运动定律和动能定理列式求解．