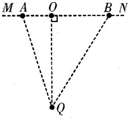
潜艇部队经常开展鱼雷攻击敌方舰艇演练.某次演习的简化模型:敌舰沿直线MN匀速航行,潜艇隐蔽在Q点不动,Q到MN的距离QO=2000m.当敌舰到达距离O点800m的A点时,潜艇沿QO方向发射一枚鱼雷,正好在O点击中敌舰.敌舰因受鱼雷攻击,速度突然减为原来的
,且立刻沿原运动方向做匀加速运动逃逸.100s后潜艇沿QB方向发射第二枚鱼雷,鱼雷在B点再次击中敌舰.测得OB=1 500m,不考虑海水速度的影响,潜艇和敌舰可视为质点,鱼雷的速度大小恒为25m/s.求:1 2
(1)敌舰第一次被击中前的速度;
(2)鱼雷由Q至B经历的时间;
(3)敌舰逃逸时的加速度大小(可用分式表示结果).
(1)鱼雷从Q到O经历的时间t1=
=QO v
=80s;2000 25
敌舰第一次被击中前的速度v1=
=AO t1
m/s=10m/s;800 80
(2)设第二枚鱼雷经过时间t2击中敌舰,则QB=
=2500m;OB2+QO2
t2=
=QB v
=100s;2500 25
(3)敌舰第一次击中后瞬间的速度
v2=
=5m/sv1 2
敌舰第一次击中后运动的时间t3=t2+100=200s;
设敌舰的加速度为a,由OB=v2t3+
at321 2
解得a=0.025m/s2;
答:(1)第一次击中前的速度为10m/s;
(2)鱼雷从Q到B的时间为100s;
(3)敌舰的加速度为0.025m/s2.
