问题
解答题
用白纸剪一些边长相同的正三角形、正方形、正五边形、正六边形。用信封A装若干个正三角形、信封B装若干个正方形、信封C装若干个正五边形、信封D装若干个正六边形。将信封A、B、C、D(信封的大小、颜色、质地完全相同)装入不透明的袋子中。
(1)随机摸出一个信封,求该信封所装正多边形能镶嵌成一个平面图案的概率;
(2)随机摸出一个信封不放回,接着再随机摸出一个信封,求同时用这两次摸出信封中的两种正多边形能镶嵌成一个平面图案的概率(用列表法或树形图法解答)。
答案
解:(1)摸出的结果共有4个,其中能镶嵌成一个平面图案(记为事件E)的有3个,即正三角形、正方形、正六边形,所以P(E)=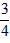 ;
;
(2)树形图如下:
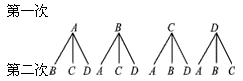
或列表如下表:
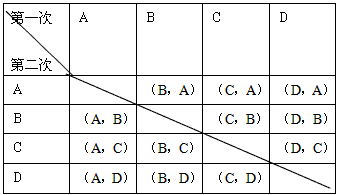
由树形图(或列表)可以看出,所有可能结果共有12个,能镶嵌成一个平面图案(记为事件F)的有4个,即AB、AD、BA、DA,所以P(F)=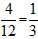 。
。
