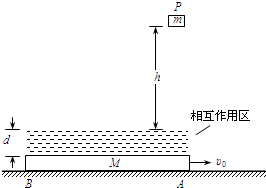
质量为M的平板长为L=0.88m,在光滑的水平面上以速度υ0 向右匀速运动,在平板上方存在厚度d=2cm的“相互作用区域”(如图中虚线部分所示),“相互作用区域”上方高h=20cm处有一质量为m的静止物块P.当平板M的右端A经过物块P正下方的瞬时,P无初速度释放.物块P以速度υ1进入相互作用区时,除重力之外,P立即受到一个竖直向上的恒力F.已知F=11mg,取重力加速度g=10m/s2,不计空气阻力.
试求:(1)物块P下落至与平板刚接触时的速度υ2多大?
(2)欲使物块P不落到平板M上,平板速度υ0应不小于多少?
(1)P先做自由落体运动,有:υ12=2gh ①
之后进入相互作用区域,受向上的恒力F和重力作用,由牛顿第二定律得:
F-mg=ma,即:11mg-mg=ma ②
P物体做匀减速运动,有:υ22-υ12=-2ad ③
由①、②、③解得 υ2=0
(2)P先做自由落体运动过程,有h=
gt1④1 2
进入相互作用区做匀减速运动的末速为零,故有d=
at2⑤1 2
且a=10g ⑥
由式④、⑤、⑥解得 t1=0.2s t2=0.02s
所以,P释放后到与平板接触经历的时间为
t=t1+t2=0.2s+0.02s=0.22s
欲使物块P不落到平板M上,应满足v0t>L,于是得:
v0>
=L t
m/s=4m/s.0.88 0.22
答:(1)物块P下落至与平板刚接触时的速度υ2为0;
(2)欲使物块P不落到平板M上,平板速度υ0应不小于4m/s.
