问题
解答题
小昆和小明相约玩一种“造数”游戏。游戏规则如下:同时抛掷一枚均匀的硬币和一枚均匀的骰子,硬币的正、反面分别表示“新数”的性质符号(约定硬币正面向上记为“+”号,反面向上记为“-”号),与骰子投出面朝上的数字组合成一个“新数”;如抛掷结果为“硬币反面向上,骰子面朝上的数字是4”,记为“-4”。
(1) 利用树状图或列表的方法(只选其中一种)表示出游戏可能出现的所有结果;
(2) 写出组合成的所有“新数”;
(3) 若约定投掷一次的结果所组合成的“新数”是3的倍数,则小昆获胜;若是4或5的倍数,则小明获胜。你觉得他们的约定公平吗?为什么?
答案
解:(1)列表如下:

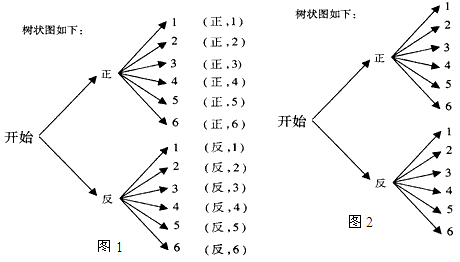
(2)组合成的“新数”为1,2,3,4,5,6,-1,-2,-3,-4,-5,-6;
(3)所有组合成的“新数”中,是3的倍数的数有:3,6,-3,-6,共4个,
∴P(3的倍数)=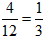 ,
,
是4或5的倍数的数有:4,5,-4,-5,
∴P(4或5的倍数)=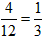 ,
,
∵两个概率相等,
∴他们的约定公平。
