问题
解答题
已知f(n)=1+
(1)当n=1,2,3时,试比较f(n)与g(n)的大小关系; (2)猜想f(n)与g(n)的大小关系,并给出证明. |
答案
(1)当n=1时,f(1)=1,g(1)=1,所以f(1)=g(1);
当n=2时,f(2)=
,g(2)=9 8
,11 8
所以f(2)<g(2);
当n=3时,f(3)=
,g(3)=251 216
,312 216
所以f(3)<g(3).
(2)由(1),猜想f(n)≤g(n),下面用数学归纳法给出证明:
①当n=1,2,3时,不等式显然成立.
②假设当n=k(k≥3)时不等式成立,
即1+
+1 23
+1 33
+1 43
<1 k3
-3 2
,1 2k2
那么,当n=k+1时,f(k+1)=f(k)+
<1 (k+1)3
-3 2
+1 2k2
,1 (k+1)3
因为
-(1 2(k+1)2
-1 2k2
)=1 (k+1)3
-k+3 2(k+1)3
=1 2k2
<0,-3k-1 2(k+1)3k2
所以f(k+1)<
-3 2
=g(k+1).1 2(k+1)2
由①、②可知,对一切n∈N*,都有f(n)≤g(n)成立.

 缺失,间隙小,切角缺损1/3,X线片检查根长大,牙周膜健康,
缺失,间隙小,切角缺损1/3,X线片检查根长大,牙周膜健康,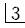 为局部义齿,最好的设计是()。
为局部义齿,最好的设计是()。