问题
解答题
在一个口袋中有4个完全相同的小球,把它们分别标上1、2、3、4.小明先随机地摸出一个小球,小强再随机的摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则:当x>y时小明获胜,否则小强获胜.
①若小明摸出的球不放回,求小明获胜的概率.
②若小明摸出的球放回后小强再随机摸球,问他们制定的游戏规则公平吗?请说明理由.
答案
解:①画树状图得:
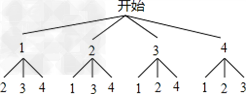
∵共有12种等可能的结果,
小明获胜的有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3)共6种情况,
∴小明获胜的概率为: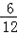 =
= ;
;
(2)画树状图得:
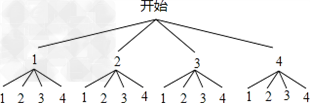
∵共有16种等可能的结果,
小明获胜的有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3)共6种情况,
∴P(小明获胜)=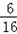 =
= ,P(小强获胜)=
,P(小强获胜)= ,
,
∵P(小明获胜)≠P(小强获胜),
∴他们制定的游戏规则不公平.
