问题
解答题
已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+3c2+6d2=5,试求a的最值.
答案
amax=2 amin=1
根据柯西不等式有(2b2+3c2+6d2)(
+
+
)≥(b+c+d)2,
即2b2+3c2+6d2≥(b+c+d)2,
由条件可得,5-a2≥(3-a)2,
解得,1≤a≤2,
当且仅当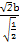
=
=
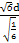时等号成立,
代入b=,c=,d=时,amax=2,
b=1,c=
,d=时,amin=1.