问题
解答题
日常生活中，某些东西所含的热量比较高，对我们的身体有一定的影响，下表给出了不同类型八种饼干的数据，第一列数据表示八种饼干各含热量的百分比，第二列数据表示顾客对八种饼干所给予分数（百分制）.
（2）求出回归直线； （3）关于两个变量之间的关系，你能得出什么结论？ （4）为什么人们更喜欢吃位于回归直线上方的饼干而不是下方的饼干？ |
答案
（1）散点图略；
（2）Ⅰ.先把数据列成表：
| 项目 品牌 | 热量百分比x | 品味记录y | x2 | y2 | xy |
| 1 | 25 | 89 | 625 | 7 921 | 2 225 |
| 2 | 34 | 89 | 1 156 | 7 921 | 3 026 |
| 3 | 20 | 80 | 400 | 6 400 | 1 600 |
| 4 | 19 | 78 | 361 | 6 084 | 1 482 |
| 5 | 26 | 75 | 676 | 5 625 | 1 950 |
| 6 | 20 | 71 | 400 | 5 041 | 1 420 |
| 7 | 19 | 65 | 361 | 4 225 | 1 235 |
| 8 | 24 | 62 | 576 | 3 844 | 1 488 |
| ∑ | 187 | 609 | 4 555 | 47 06 | 14 426 |
Ⅱ.计算b,a的值：
由上表分别计算x，y的平均数得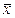
=
,
=
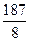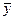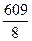，代入公式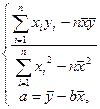
，得（注意：不必把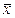=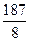,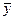=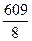化为小数，以减小误差）
b=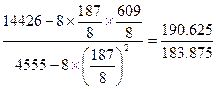
=1.036710,
a=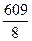-1.036 710×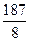="76.125-24.233" 1="51.891" 9.
Ⅲ.写出回归直线方程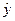
=51.9+1.037x．
（3）回归直线方程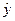=51.9+1.037x中的回归系数b=1.037，它的意义是：热量比每增加一个百分比，口味记录平均增加1.037分．
（4）人们之所以喜欢吃位于回归直线上方的饼干而不是下方的饼干，是因为饼干所含有的热量百分比相同时，人们的满意率比较高；并且满意率相同时，位于回归直线上方的饼干所含有热量百分比较低，人们比较喜欢吃热量百分比较低的食品．
本题运用了回归直线方程的求法，以及回归直线方程的应用．