5≤f(-2)≤10

方法一 设f(-2)=mf(-1)+nf(1) (m,n为待定系数),

则4a-2b=m(a-b)+n(a+b),

即4a-2b=(m+n)a+(n-m)b,

于是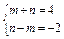得,解得,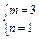

∴f(-2)=3f(-1)+f(1).

又∵1≤f(-1)≤2,2≤f(1)≤4,

∴5≤3f(-1)+f(1)≤10,

故5≤f(-2)≤10.

方法二 由,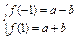

得,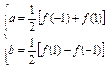

∴f(-2)=4a-2b=3f(-1)+f(1).

又∵1≤f(-1)≤2,2≤f(1)≤4,

∴5≤3f(-1)+f(1)≤10,故5≤f(-2)≤10.

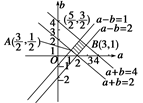
方法三 由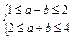确定的平面区域如图.

当f(-2)=4a-2b过点A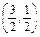时,

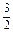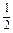取得最小值4×-2×=5,

当f(-2)=4a-2b过点B(3,1)时,

取得最大值4×3-2×1=10,

∴5≤f(-2)≤10.