a＜c＜b

∵bc＞a²＞0,∴b,c同号.

又a²+c²＞0,a＞0,∴b=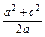＞0,∴c＞0,

由(a-c)²=2ab-2ac=2a(b-c)≥0,∴b-c≥0.

当b-c＞0,即b＞c时,

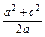由得·c＞a²

即(a-c)(2a²+ac+c²)＜0.

∵a＞0,b＞0,c＞0,∴2a²+ac+c²＞0,

∴a-c＜0,即a＜c,则a＜c＜b；

当b-c=0,即b=c时,

∵bc＞a²,∴b²＞a²,即b≠a.

又∵a²-2ab+c²=(a-b)²=0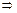a=b与a≠b矛盾,

∴b-c≠0.

综上可知:a＜c＜b.