已知－1＜a+b＜3且2＜a－b＜4，求2a+3b的取值范围.
－
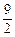＜2a+3b＜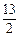
∵a+b，a－b的范围已知，
∴要求2a+3b的取值范围，
只需将2a+3b用已知量a+b，a－b表示出来.
可设2a+3b=x（a+b）+y（a－b），用待定系数法求出x、y.
设2a+3b=x（a+b）+y（a－b），
∴
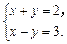解得
∴－
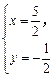
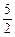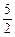＜（a+b）＜
，
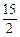－2＜－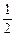
（a－b）＜－1.
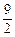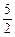∴－＜（a+b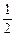）－（a－b）＜，
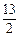即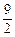－＜2a+3b＜.
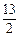错解：解此题常见错误是：－1＜a+b＜3， ①
2＜a－b＜4. ②
①+②得1＜2a＜7. ③
由②得－4＜b－a＜－2. ④
①+④得－5＜2b＜1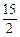，∴－＜3b＜
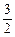. ⑤
③+⑤得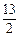－＜2a+3b＜
.
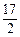Google Inc. introduced plans in June to offer 3-D maps of major cities and other new features for its popular Google Maps and Google Earth services. New features include the ability to _____50_____ portions of Google Maps onto phones and other _____51_____ devices, with detailed data, so users can find their way around _____52_____ areas even if they don’t have an active Internet connection. Perhaps the most _____53_____ new feature was the detailed three-dimensional images that Google plans to offer for major cities in coming months. Google product manager Peter Birch explained that the company is using _____54_____ to obtain detailed images of every street and building in an area, from different _____55_____, which are then compiled into images that appear to show height, depth and even architectural details of buildings and streets, _____56_____ landscape features such as trees. “We are trying to create the effect that you are flying _____57_____ the city, almost as if you were in your own personal helicopter,” said Birch. Compiling those images _____58_____ extensive photographing and processing of images, however. _____59_____ Birch promised to have images _____60_____ for several major cities in coming months, he and other Google officials did not offer a detailed timetable. Industry blogs have reported that Apple is preparing to _____61_____ its own maps and navigation service, including 3-D images. Analysts say the _____62_____ is part of a larger race between the two tech giants to offer services that keep users _____63_____ and allow each company to deliver advertising or other products targeted to specific locations and other data on ____64______ interests.
|