问题
解答题
某渔业公司今年初用98万元购进一艘渔船用于捕捞，第一年需各种费用12万元，从第二年开始包括维修费在内，每年所需费用均比上一年增加4万元，该船每年捕捞的总收入为50万元.
(1)该船捕捞几年开始盈利(即总收入减去成本及所有费用之差为正值)？
(2)该船捕捞若干年后，处理方案有两种:
①当年平均盈利达到最大值时，以26万元的价格卖出；
②当盈利总额达到最大值时，以8万元的价格卖出.
问哪一种方案较为合算，请说明理由.
答案
(1)设捕捞3年后，开始盈利.
(2)①经过7年捕捞后年平均利润最大，共盈利12×7+26=110万元.
②∵两种方案获利相等，但方案②的时间长，所以方案①合算.
(1)设捕捞n年后开始盈利，盈利为y元，则
y=50n－［12n+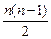
×4］－98
=－2n2+40n－98.
由y＞0，得n2－20n+49＜0.
∴10－
＜n＜10+ (n∈N).
∴3≤n≤17.∴n=3,
即捕捞3年后，开始盈利.
(2)①平均盈利为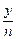
=－2n－
+40≤－2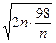
+40=12，
当且仅当2n=,即n=7时，年平均利润最大.
∴经过7年捕捞后年平均利润最大，共盈利12×7+26=110万元.
②∵y=－2n2+40n－98=－2(n－10)2+102，
∴当n=10时，y的最大值为102,
即经过10年捕捞盈利额最大，共盈利102+8=110万元.
故两种方案获利相等，但方案②的时间长，所以方案①合算.
