问题
填空题
函数f(x)＝|x2－a|在区间[－1,1]上的最大值M(a)的最小值是________．
答案
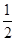
依题意得，当a≤0，x∈[－1,1]时，f(x)＝|x2－a|＝x2－a的最大值M(a)＝1－a∈[1，＋∞)；当a≥1，x∈[－1,1]时，f(x)＝|x2－a|＝a－x2的最大值M(a)＝a∈[1，＋∞)；当0<a≤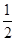，x∈[－1,1]时，f(x)＝|x2－a|的最大值M(a)＝1－a∈
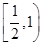；当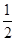<a<1，x∈[－1,1]时，f(x)＝|x2－a|的最大值M(a)＝a∈
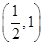.综上可知，M(a)的最小值是.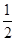