问题
选择题
对于实数x,当n≤x<n+1(n∈Z)时,规定[x]=n,则不等式4[x]2-36[x]+45<0的解集为( )
A.{x|2≤x<8}
B.{x|2<x≤8}
C.{x|2≤x≤8}
D.{x|2<x<8}
答案
答案:A
先利用换元法将不等式化为一元二次不等式,求得[x]的范围,再结合[x]的含义得出x的范围.
令t=[x],则不等式化为4t2-36t+45<0,解得 <t<
<t<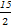 ,而t=[x],所以
,而t=[x],所以 <[x]<
<[x]<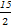 ,由[x]的定义可知x的取值范围是2≤x<8,即不等式解集为{x|2≤x<8}.
,由[x]的定义可知x的取值范围是2≤x<8,即不等式解集为{x|2≤x<8}.
