问题
解答题
若0<a<2,0<b<2,0<c<2,求证:(2-a)b,(2-b)c,(2-c)a不能同时大于1.
答案
见解析
证明:假设(2-a)b>1,(2-b)c>1,(2-c)a>1,
由题意知2-a>0,2-b>0,2-c>0,
那么 ≥
≥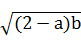 >1.
>1.
同理, >1,
>1,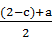 >1,
>1,
三式相加,得3>3矛盾,所以假设不成立.
所以(2-a)b,(2-b)c,(2-c)a不能同时大于1.
若0<a<2,0<b<2,0<c<2,求证:(2-a)b,(2-b)c,(2-c)a不能同时大于1.
见解析
证明:假设(2-a)b>1,(2-b)c>1,(2-c)a>1,
由题意知2-a>0,2-b>0,2-c>0,
那么 ≥
≥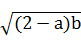 >1.
>1.
同理, >1,
>1,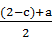 >1,
>1,
三式相加,得3>3矛盾,所以假设不成立.
所以(2-a)b,(2-b)c,(2-c)a不能同时大于1.