问题
解答题
已知函数f(x)=|x+3|+|x-a|(a>0).
(1)当a=4时,已知f(x)=7,求x的取值范围;
(2)若f(x)≥6的解集为{x|x≤-4或x≥2},求a的值.
答案
(1)x∈[-3,4](2)a=1
(1)因为|x+3|+|x-4|≥|x+3-x+4|=7,当且仅当(x+3)(x-4)≤0时等号成立.
所以f(x)=7时,-3≤x≤4,故x∈[-3,4].
(2)由题知f(x)=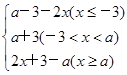 ,
,
当a+3≥6时,不等式f(x)≥6的解集为R,不合题意;
当a+3<6时,不等式f(x)≥6的解为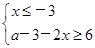 或
或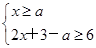 ,
,
即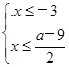 或
或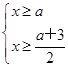
又因为f(x)≥6的解集为{x|x≤-4或x≥2},所以a=1.
