问题
解答题
甲布袋中有三个红球,分别标有数字1,2,3;乙布袋中有三个白球,分别标有数字2,3,4.这些球除颜色和数字外完全相同.小亮从甲袋中随机摸出一个红球,小刚从乙袋中随机摸出一个白球.
(1)用画树状图(树形图)或列表的方法,求摸出的两个球上的数字之和为6的概率;
(2)小亮和小刚做游戏,规则是:若摸出的两个球上的数字之和为奇数,小亮胜;否则,小刚胜.你认为这个游戏公平吗?为什么?
答案
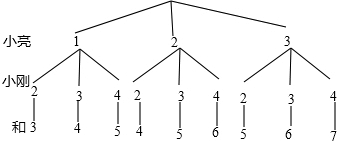
(1)解法一:树状图
(3分)
∴P(两个球上的数字之和为6)=
.(2分)2 9
解法二:列表
| 2 | 3 | 4 | |
| 1 | (1,2) | (1,3) | (1,4) |
| 2 | (2,2) | (2,3) | (2,4) |
| 3 | (3,2) | (3,3) | (3,4) |
| 2 |
| 9 |
(2)不公平.(1分)
∵P(小亮胜)=
,P(小刚胜)=5 9
.(2分)4 9
∴P(小亮胜)≠P(小刚胜).
∴这个游戏不公平.(2分)
