问题
解答题
已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.
答案
见解析
【证明】假设a,b,c,d都是非负数,因为a+b=c+d=1,
所以a,b,c,d∈[0,1],
所以ac≤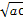 ≤
≤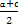 ,bd≤
,bd≤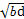 ≤
≤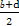 ,
,
所以ac+bd≤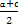 +
+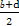 =1,
=1,
这与已知ac+bd>1相矛盾,所以原假设不成立,即证得a,b,c,d中至少有一个是负数.
已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.
见解析
【证明】假设a,b,c,d都是非负数,因为a+b=c+d=1,
所以a,b,c,d∈[0,1],
所以ac≤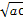 ≤
≤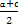 ,bd≤
,bd≤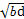 ≤
≤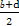 ,
,
所以ac+bd≤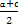 +
+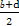 =1,
=1,
这与已知ac+bd>1相矛盾,所以原假设不成立,即证得a,b,c,d中至少有一个是负数.