见解析

(1)当n＝5时，2⁵>5²，结论成立．

(2)假设当n＝k(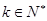，k≥5)时，结论成立，即有2^k>k²，

那么当n＝k＋1时，左边＝2^k＋1＝2·2^k>2·k²＝(k＋1)²＋(k²－2k－1)＝(k＋1)²＋(k－1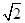－)(k－1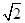＋)>(k＋1)²＝右边.

∴也就是说，当n＝k＋1时，结论成立．

∴由(1)、(2)可知，不等式2ⁿ>n²对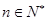，n≥5时恒成立．