问题
填空题
若正数a,b满足ab=a+b+3,则ab的取值范围是 .
答案
[9,+∞)
令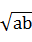
=t(t>0),由ab=a+b+3≥2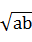+3,则t2≥2t+3,所以t≥3或t≤-1(舍去),所以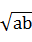≥3,ab≥9,当a=b=3时取等号.
搜题请搜索小程序“爱下问搜题”
若正数a,b满足ab=a+b+3,则ab的取值范围是 .
[9,+∞)
令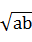=t(t>0),由ab=a+b+3≥2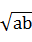+3,则t2≥2t+3,所以t≥3或t≤-1(舍去),所以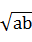≥3,ab≥9,当a=b=3时取等号.