问题
解答题
若实数x、y、z满足x＋2y＋3z＝a(a为常数)，求x2＋y2＋z2的最小值．
答案
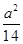
∵(12＋22＋32)(x2＋y2＋z2)≥(x＋2y＋3z)2＝a2，即14(x2＋y2＋z2)≥a2，
∴x2＋y2＋z2≥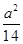，即x2＋y2＋z2的最小值为.
搜题请搜索小程序“爱下问搜题”
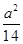若实数x、y、z满足x＋2y＋3z＝a(a为常数)，求x2＋y2＋z2的最小值．
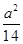
∵(12＋22＋32)(x2＋y2＋z2)≥(x＋2y＋3z)2＝a2，即14(x2＋y2＋z2)≥a2，
∴x2＋y2＋z2≥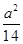，即x2＋y2＋z2的最小值为.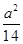