问题
解答题
已知x,y,z∈R+,且x+y+z=1
(1)若2x2+3y2+6z2=1,求x,y,z的值.
(2)若2x2+3y2+tz2≥1恒成立,求正数t的取值范围.
答案
(1)x=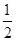 ,y=
,y=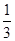 ,z=
,z= (2)t≥6
(2)t≥6
(1)∵(2x2+3y2+6z2)(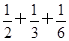 )≥(x+y+z)2=1,当且仅当
)≥(x+y+z)2=1,当且仅当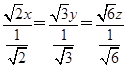 时取“=”.∴2x=3y=6z,
时取“=”.∴2x=3y=6z,
又∵x+y+z=1,∴x=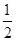 ,y=
,y=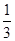 ,z=
,z= .
.
(2)∵(2x2+3y2+tz2)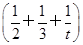 ≥(x+y+z)2=1,∴(2x2+3y2+tz2)min=
≥(x+y+z)2=1,∴(2x2+3y2+tz2)min= .
.
∵2x2+3y2+tz2≥1恒成立,∴ ≥1.∴t≥6.
≥1.∴t≥6.
