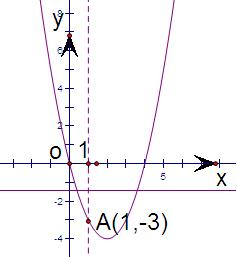问题
选择题
不等式x2﹣4x+a<0存在小于1的实数解,则实数a的取值范围是( )
A.(﹣∞,4)
B.(﹣∞,4]
C.(﹣∞,3)
D.(﹣∞,3]
答案
答案:C
不等式x2﹣4x+a<0可化为:
x2﹣4x<﹣a,
设y=x2﹣4x,y=﹣a,分别画出这两个函数的图象,如图,
由图可知,不等式x2﹣4x+a<0存在小于1的实数解,
则有:﹣a>﹣3.
故a<3.
故选C.
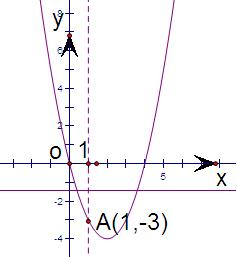
不等式x2﹣4x+a<0存在小于1的实数解,则实数a的取值范围是( )
A.(﹣∞,4)
B.(﹣∞,4]
C.(﹣∞,3)
D.(﹣∞,3]
答案:C
不等式x2﹣4x+a<0可化为:
x2﹣4x<﹣a,
设y=x2﹣4x,y=﹣a,分别画出这两个函数的图象,如图,
由图可知,不等式x2﹣4x+a<0存在小于1的实数解,
则有:﹣a>﹣3.
故a<3.
故选C.