问题
解答题
函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围;
(2)当x∈[-2,2]时,f(x)≥a恒成立,求a的取值范围.
答案
(1)[-6,2](2)[-7,2]
(1)∵x∈R,f(x)≥a恒成立,
∴x2+ax+3-a≥0恒成立,则Δ=a2-4(3-a)≤0,得-6≤a≤2.
∴当x∈R时,f(x)≥a恒成立,则a的取值范围为[-6,2].
(2)f(x)=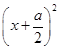 +3-
+3-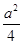 .
.
讨论对称轴与[-2,2]的位置关系,得到a的取值满足下列条件:
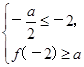 或
或 或
或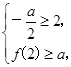
即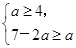 或
或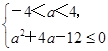 或
或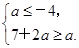
解得-7≤a≤2.∴当x∈[-2,2]时,f(x)≥a恒成立,则a的取值范围为[-7,2].
