问题
解答题
求证：a2＋b2≥ab＋a＋b－1.
答案
见解析
∵(a2＋b2)－(ab＋a＋b－1)＝a2＋b2－ab－a－b＋1
＝
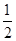(2a2＋2b2－2ab－2a－2b＋2)
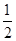＝[(a2－2ab＋b2)＋(a2－2a＋1)＋(b2－2b＋1)]
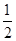＝[(a－b)2＋(a－1)2＋(b－1)2]≥0.
∴a2＋b2≥ab＋a＋b－1.
搜题请搜索小程序“爱下问搜题”
求证：a2＋b2≥ab＋a＋b－1.
见解析
∵(a2＋b2)－(ab＋a＋b－1)＝a2＋b2－ab－a－b＋1
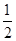＝(2a2＋2b2－2ab－2a－2b＋2)
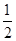＝[(a2－2ab＋b2)＋(a2－2a＋1)＋(b2－2b＋1)]
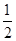＝[(a－b)2＋(a－1)2＋(b－1)2]≥0.
∴a2＋b2≥ab＋a＋b－1.