问题
解答题
用分析法证明:当x>1时,x>ln(1+x).
答案
见解析
证明:当x>1时,要证x>ln(1+x),即证f(x)= x-ln(1+x)>0=f(0),即证f'(x)=1-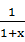
=
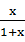>0,显然x>1时,f'(x)>0,所以原命题成立.
搜题请搜索小程序“爱下问搜题”
用分析法证明:当x>1时,x>ln(1+x).
见解析
证明:当x>1时,要证x>ln(1+x),即证f(x)= x-ln(1+x)>0=f(0),即证f'(x)=1-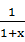=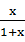>0,显然x>1时,f'(x)>0,所以原命题成立.