问题
填空题
定义在R上的运算:x*y=x(1-y),若不等式(x-y)*(x+y)<1对一切实数x恒成立,则实数y的取值范围是 .
答案
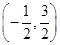
∵(x-y)*(x+y)=(x-y)(1-x-y)
=x-x2-y+y2
<1,
∴-y+y2<x2-x+1,要使该不等式对一切实数x恒成立,则需有-y+y2<(x2-x+1)min=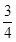
,
解得-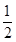
<y<
.
搜题请搜索小程序“爱下问搜题”
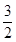定义在R上的运算:x*y=x(1-y),若不等式(x-y)*(x+y)<1对一切实数x恒成立,则实数y的取值范围是 .
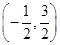
∵(x-y)*(x+y)=(x-y)(1-x-y)
=x-x2-y+y2
<1,
∴-y+y2<x2-x+1,要使该不等式对一切实数x恒成立,则需有-y+y2<(x2-x+1)min=,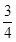
解得-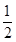<y<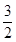.