问题
填空题
设0≤α≤π,不等式8x2-(8sinα)x+cos2α≥0对x∈R恒成立,则α的取值范围为 .
答案
[0,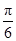 ]∪[
]∪[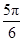 ,π]
,π]
因为不等式对一切实数恒成立,
所以Δ=64sin2α-32cos2α≤0,
即2sin2α-cos2α≤0,
由2sin2α=1-cos2α,得1-2cos2α≤0,
所以cos2α≥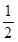 ,又α∈[0,π],2α∈[0,2π],
,又α∈[0,π],2α∈[0,2π],
所以2α∈[0,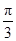 ]∪[
]∪[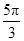 ,2π],
,2π],
即α∈[0,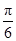 ]∪[
]∪[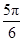 ,π].
,π].

 与小李工资的
与小李工资的 的和比小陈工资的
的和比小陈工资的