问题
选择题
设x,y∈R+,且满足x+4y=40,则lgx+lgy的最大值为 ( )
A．40
B．10
C．4
D．2
答案
答案：D
选D.因为x,y∈R+,所以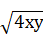
≤
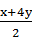,当且仅当x=4y=20时,等号成立.所以
≤
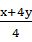=10,所以xy≤100,所以lgx+lgy=lg(xy)≤lg100=2.
搜题请搜索小程序“爱下问搜题”
设x,y∈R+,且满足x+4y=40,则lgx+lgy的最大值为 ( )
A．40
B．10
C．4
D．2
答案：D
选D.因为x,y∈R+,所以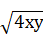≤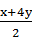,当且仅当x=4y=20时,等号成立.所以≤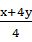=10,所以xy≤100,所以lgx+lgy=lg(xy)≤lg100=2.