问题
填空题
已知f(x)=|log3x|,若f(a)=f(b)且a≠b,则a+b的取值范围是______.
答案
根据题意,对于f(x)=|log3x|,有x>0,
若f(a)=f(b),则|log3a|=|log3b|,
又由a≠b,则有log3a=-log3b,即log3a+log3b=log3ab=0,
则ab=1,
又由a、b>0且a≠b,
则a+b>2
=2,ab
即a+b的取值范围是(2,+∞);
故答案为(2,+∞).

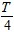 时(T为交流的周期),原线圈中的电流瞬时值为0.03A.变压器的原、副线圈的匝数比为( )
时(T为交流的周期),原线圈中的电流瞬时值为0.03A.变压器的原、副线圈的匝数比为( )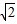
 :3
:3