问题
填空题
若关于x的不等式ax2-|x+1|+2a<0的解集为空集,则实数a的取值范围是 .
答案

当x>-1时,
原不等式可化为ax2-x+2a-1<0,
由题意知该不等式的解集为空集,
结合二次函数的图象可知a>0且Δ=1-4a(2a-1)≤0,
解得a≥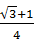 ;
;
当x≤-1时,原不等式可化为ax2+x+1+2a<0.
由题意知该不等式的解集为空集,结合二次函数的图象可知a>0且Δ=1-4a(2a+1)≤0,解得a≥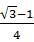 .
.
综上可知,a≥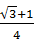 .
.
