问题
解答题
若数列A：a1，a2，…，an（n≥2）满足|ak+1-ak|=1 （k=1，2，…，n-1），则称An为E数列。记S（An）=a1+a2+…+an。
（Ⅰ）写出一个E数列A5满足a1=a3=0；
（Ⅱ）若a1=12，n=2000，证明：E数列An是递增数列的充要条件是an=2011；
（Ⅲ）在a1=4的E数列An中，求使得S（An）=0成立的n的最小值。
答案
解：（Ⅰ）0，1，0，1，0是一具满足条件的E数列A5（答案不唯一）；
（Ⅱ）必要性：因为E数列An是递增数列，
所以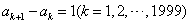
，
所以An是首项为12，公差为1的等差数列，
所以a2000=12+（2000-1）×1=2011；
充分性：由于a2000-a1999≤1，
a1999-a1998≤1，
…… ，
a2-a1≤1，
所以a2000-a1≤1999，
即a2000≤a1+1999，
又因为a1=12，a2000=2011， 所以a2000=a1+1999，
故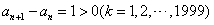
，即An是递增数列；
综上，结论得证。
（Ⅲ）对于首项为4的数列An，由于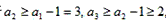
，…，a8≥a7-1≥-3，
所以，所以a1+a2+…+ak＞0（k=2，3，…，8），
所以对任意的首项为4的E数列An，
若S（An）=0，则必有n≥9，
又a1=4的E数列A9：4，3，2，1，0，-1，-2，-3，-4满足S（A9）=0，
所以n的最小值是9．