问题
解答题
知x>0,y>0,x+2y+xy=30,求xy的取值范围.
答案
(0,18]
因为x>0,y>0,所以30=x+2y+xy
≥2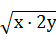 +xy=2
+xy=2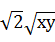 +xy,
+xy,
所以(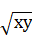 )2+2
)2+2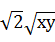 -30≤0,
-30≤0,
所以(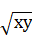 -3
-3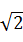 )(
)(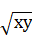 +5
+5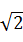 )≤0,
)≤0,
所以0<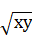 ≤3
≤3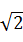 ,即0<xy≤18,
,即0<xy≤18,
当且仅当x=2y,即x=6,y=3时等号成立.
所以xy的取值范围为(0,18].
【一题多解】本题还可用消元的方法:
因为x+2y+xy=30,所以y=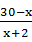 ,
,
所以xy=x·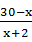 =
=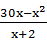
=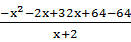
=-x+32-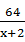 =-(x+2)-
=-(x+2)-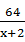 +34,
+34,
又因为x>0,
所以(x+2)+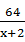 ≥2
≥2 =16,
=16,
当且仅当x+2=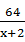 ,即x=6时,等号成立,
,即x=6时,等号成立,
所以xy≤-16+34=18,
当且仅当x=6,y=3时等号成立.
所以xy的取值范围是(0,18].
