问题
解答题
已知a,b,c∈{正实数},且a2+b2=c2,当n∈N,n>2时比较cn与an+bn的大小.
答案
an+bn<cn.
解:∵a,b,c∈{正实数},∴an,bn,cn>0,
而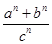 =(
=(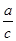 )n+(
)n+(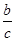 )n.
)n.
∵a2+b2=c2,则(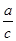 )2+(
)2+(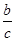 )2=1,
)2=1,
∴0<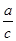 <1,0<
<1,0<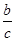 <1.
<1.
∵n∈N,n>2,
∴(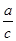 )n<(
)n<(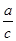 )2,(
)2,(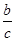 )n<(
)n<(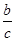 )2,
)2,
∴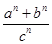 =(
=(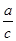 )n+(
)n+(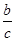 )n<
)n<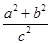 =1,
=1,
∴an+bn<cn.
已知a,b,c∈{正实数},且a2+b2=c2,当n∈N,n>2时比较cn与an+bn的大小.
an+bn<cn.
解:∵a,b,c∈{正实数},∴an,bn,cn>0,
而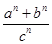 =(
=(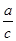 )n+(
)n+(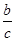 )n.
)n.
∵a2+b2=c2,则(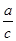 )2+(
)2+(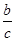 )2=1,
)2=1,
∴0<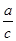 <1,0<
<1,0<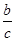 <1.
<1.
∵n∈N,n>2,
∴(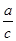 )n<(
)n<(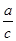 )2,(
)2,(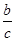 )n<(
)n<(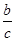 )2,
)2,
∴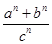 =(
=(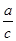 )n+(
)n+(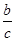 )n<
)n<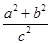 =1,
=1,
∴an+bn<cn.