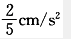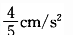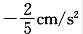问题
解答题
对于函数f(x),其定义域为D,若任取x1、x2∈D,且x1≠x2,若f(
(1)设f(x)=ax2(a>0),试判断f(x)是否为其定义域上的凸函数,并说明原因; (2)若函数f(x)=㏒ax(a>0,且a≠1)为其定义域上的凸函数,试求出实数a的取值范围. |
答案
(1)f(x)不是其定义域上的凸函数.
f(x)的定义域为R,设x1≠x2,则
f(
)-x1+x2 2
[f(x1)+f(x2)]=a(1 2
)2-x1+x2 2
(ax12-ax22)=-1 2
<0,…2分a(x1-x2)2 4
∴f(
)<x1+x2 2
[f(x1)+f(x2)],…4分1 2
∴f(x)不是其定义域上的凸函数…6分
(2)∵f(x)的定义域为(0,+∞),且f(x)在(0,+∞)内是凸函数,
∴f(
)>x1+x2 2
[f(x1)+f(x2)],…8分1 2
即loga
>x1+x2 2
(logax1+logax2)=loga1 2
①…10分x1x2
∵x1、x2∈(0,+∞),且x1≠x2,
∴(
)2-x1x2=x1+x2 2
>0,即(x1-x2)2 4
>x1+x2 2
…12分x1x2
故要①成立,则a>1.
∴实数a的取值范围是(1,+∞)…14分