问题
问答题
A．条件(1)充分，但条件(2)不充分．
B．条件(2)充分，但条件(1)不充分．
C．条件(1)和(2)单独都不充分，但条件(1)和条件(2)联合起来充分．
D．条件(1)充分，条件(2)也充分．
E．条件(1)和(2)单独都不充分，条件(1)和条件(2)联合起来也不充分．
若x，y，z∈R，则|x|+|y|+|z|的最小值为4．
(1)x+y+z=0； (2)xyz=2．
答案
参考答案：
(C)．
解析：
条件(1)中，令x=y=-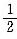
，z=1，则|x|+|y|+|z|=2，条件(1)不充分．
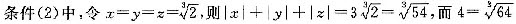，所以|x|+|y|+|z|的最小值不是4，条件(2)不充分．将条件(1)、条件(2)联合起来，由条件(2)知x，y，z负的个数是偶数，再由条件(1)知x，y，z有正有负，从而x，y，z两负一正．不妨设x＜0，y＜0，z＞0，令
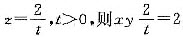，xy=t，由于L=|x|+|y|+|x+y|是关于x，y的对称式，当且仅当x=y时取得最值.可设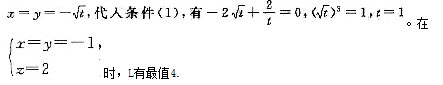
由x，y同号，有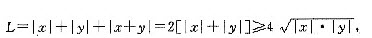
因而在x=y=-1，z=2时，L取得最小值4．条件(1)、条件(2)联合起来充分．故选(C)．
